Advertisements
Advertisements
प्रश्न
A building is in the form of a cylinder surrounded by a hemispherical dome. The base diameter of the dome is equal to \[\frac{2}{3}\] of the total height of the building . Find the height of the building , if it contains \[67\frac{1}{21} m^3\].
Advertisements
उत्तर
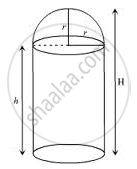
Let the radius of the dome be r.
Diameter be d.
Let the height of the building be H.
Given \[d = \frac{2}{3}H\]
\[\Rightarrow 2r = \frac{2}{3}H\]
\[ \Rightarrow r = \frac{H}{3}\]
\[ \Rightarrow 3r = H\]
Also, h + r = H
\[\Rightarrow 3r = h + r\]
\[ \Rightarrow 2r = h\]
\[ \Rightarrow r = \frac{h}{2}\]
Volume of air = Volume of air in the cylinder + Volume of air int he hemispherical dome
\[\Rightarrow \pi r^2 h + \frac{2}{3} \pi r^3 = 67\frac{1}{21}\]
\[ \Rightarrow \pi \left( \frac{h}{2} \right)^2 h + \frac{2}{3}\pi \left( \frac{h}{2} \right)^3 = \frac{1408}{21}\]
\[ \Rightarrow h^3 = \frac{11264}{176} = 64\]
\[ \Rightarrow h = 4 m\]
Hence, the radius will be \[r = \frac{h}{2} = \frac{4}{2} = 2 m\]
Height of the building, H = 3r = \[3 \times 2 = 6 m\]
