Question

A building is in the form of a cylinder surrounded by a hemispherical dome. The base diameter of the dome is equal to  \[\frac{2}{3}\] of the total height of the building . Find the height of the building , if it contains  \[67\frac{1}{21} m^3\].

Answer 1

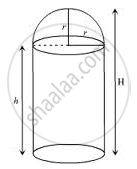
Let the radius of the dome be r. 
Diameter be d.
Let the height of the building be H.
Given  \[d = \frac{2}{3}H\]

\[\Rightarrow 2r = \frac{2}{3}H\]

\[ \Rightarrow r = \frac{H}{3}\]

\[ \Rightarrow 3r = H\]

Also, h + r = H

\[\Rightarrow 3r = h + r\]

\[ \Rightarrow 2r = h\]

\[ \Rightarrow r = \frac{h}{2}\]

Volume of air = Volume of air in the cylinder + Volume of air int he hemispherical dome

\[\Rightarrow \pi r^2 h + \frac{2}{3} \pi r^3 = 67\frac{1}{21}\]

\[ \Rightarrow \pi \left( \frac{h}{2} \right)^2 h + \frac{2}{3}\pi \left( \frac{h}{2} \right)^3 = \frac{1408}{21}\]

\[ \Rightarrow h^3 = \frac{11264}{176} = 64\]

\[ \Rightarrow h = 4 m\]

Hence, the radius will be \[r = \frac{h}{2} = \frac{4}{2} = 2 m\]

Height of the building, H = 3r =  \[3 \times 2 = 6 m\]