Advertisements
Advertisements
Question
A pen stand made of wood is in the shape of a cuboid with four conical depression and a cubical depression to hold the pens and pins , respectively . The dimension of the cuboid are \[10 cm \times 5 cm \times 4 cm\].
The radius of each of the conical depression is 0.5 cm and the depth is 2.1 cm . The edge of the cubical depression is 3 cm . Find the volume of the wood in the entire stand.
Solution
The dimensions of the cuboid = 10 cm × 5 cm × 4 cm
Volume of the total cuboid = 10 cm × 5 cm × 4 cm = 200 cm3
Radius of the conical depressions, r = 0.5 cm
Depth, h = 2.1 cm
Volume of the conical depression =
\[\frac{1}{3} \pi r^2 h = \frac{1}{3}\pi \left( 0 . 5 \right)^2 \left( 2 . 1 \right) = 0 . 5495\]cm3
Edge of cubical depression, a = 3 cm
Volume of the cubical depression = \[a^3 = 3^3 = 27 c m^3\]
Volume of wood used to make the entire stand = Volume of the total cuboid − volume of conical depression − volume of cubical depression
\[= 200 - 4 \times 0 . 5495 - 27\]
\[ = 170 . 802 c m^3 \]
APPEARS IN
RELATED QUESTIONS
A hemispherical tank full of water is emptied by a pipe at the rate of \[\frac{25}{7}\] litres per second. How much time will it take to half-empty the tank, If the tank is 3 metres in diameter?
A sphere and a cube have equal surface areas. What is the ratio of the volume of the sphere to that of the cube?
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
The rain water from a roof of 44 m × 20 m drains into a cylindrical tank having diameter of base 4 m and height 3.5 m. If the tank is just full, then find the rainfall in cm.
In a corner of a rectangular field with dimensions 35m × 22 m, a well with 14 m inside diameter is dug 8 m deep. The earth dug out is spread evenly over the remaining part of the field. Find the rise in the level of the field.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total
surface area of the toy.
The height of a conical tent is 14 m and its floor area is 346.5 m2. How much canvas, 1.1 wide, will be required for it?
A medicine capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is ______.
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the figure is `(pir^2)/3 [3h - 2r]`.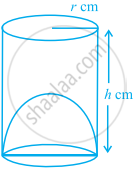
A running track has 2 semicircular ends of radius 63 m and two straight lengths. The perimeter of the track is 1000 m. Find each straight length.
