Advertisements
Advertisements
Question
The height of a conical tent is 14 m and its floor area is 346.5 m2. How much canvas, 1.1 wide, will be required for it?
Options
490 m
525 m
665 m
860 m
Solution
525 m
Area of the floor of a conical tent= πr2
Therefore,
πr2 = 346.5
`=> 22/7xx"r"^2 = 346.5`
`=> "r"^2 =((3465)/10xx7/22)`
`=> "r"^2 = 441/4`
`=> "r"^2 = (21/2)^2`
`=> "r" = 21/2 "m"`
Height of the cone = 14 m
Slant height of the cone,`"l"=sqrt("r"^2 + "h"^2)`
`=sqrt((21/2)^2) + (14)^2`
`=sqrt(441/4) + 196`
`=sqrt(1224)/4`
`=35/4 "m"`
Area of the canvas = curved surface area of the conical tent
= πrl
`=(22/7xx21/2xx35/2)`
= 577.5 m2
`"Length of the canvas" ="Area of the canvas"/"width of the canvas"`
`= 577.5/1.1 "m"`
= 525 m
APPEARS IN
RELATED QUESTIONS
A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5m and height 21m and the cone has a slant height 8m. Calculate total surface area and volume of the rocket?
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each of the hemispherical ends is 7 cm, find the cost of polishing its surface at the rate of Rs 10 per dm2 .
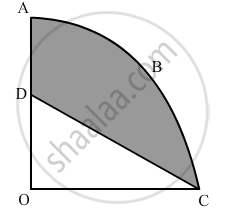
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
A tent of height 8.25 m is in the form of a right circular cylinder with diameter of base 30 m and height 5.5 m, surmounted by a right circular cone of the same base. Find the cost of the canvas of the tent at the rate of Rs 45 per m2.
The slant height of a conical mountain is 2.5 km and the area of its base is 1.54 km2. Find the height of the mountain.
Choose the correct answer of the following question:
The surface areas of two spheres are in the ratio 16 : 9. The ratio of their volumes is
The length of the longest pole that can be kept in a room (12 m × 9 m ×8 m) is
The total surface area of a hemisphere of radius 7 cm is
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each hemispherical end is 7 cm, find the surface area of the solid.
The surface area of a sphere is 616 sq cm. Find its radius tan β = `3/4`
