Advertisements
Advertisements
Question
The diameter of a sphere is 14 cm. Its volume is
Options
1428 cm3
1439 cm3
`1437 1/3 "cm"^3`
1440 cm3
Solution
`1437 1/3 "cm"^3`
Volume of the sphere`=4/3 pi"r"^3`
`= (4/3xx22/7xx7xx7xx7) "cm"^3 ["d" = 14 "cm" => "r" = 14/2 "cm" = 7 "cm"]`
`=4312/3 "cm"^3`
`=1437 1/3 "cm"^3 `
APPEARS IN
RELATED QUESTIONS
A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much is canvas cloth required to just cover the heap?
The diameters of internal and external surfaces of hollow spherical shell are 10cm and 6cm respectively. If it is melted and recast into a solid cylinder of length of 2`2/3`cm, find the
diameter of the cylinder.
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
A hemispherical depression is cut out from one face of a cubical block of side 7 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Find the surface area of the remaining solid. [Use π = \[\frac{22}{7}\]]
Choose the correct answer of the following question:
If the radius of a sphere becomes 3 times, then its volume will become
A mason constructs a wall of dimensions (270 cm × 300 cm × 350 cm) with bricks, each of size (22.5 cm × 11.25 cm × 8.75 cm) and it is assumed that `1/8` space is covered by the mortar. Number of bricks used to construct the wall is ______.
A hemispherical bowl of internal radius 9 cm is full of water. This water is to be filled in cylindrical bottles of diameter 3 cm and height 4 cm. Find the number of bottles needed in which the water can be filled.
In the given figure, AB is the diameter of a circle with center O and OA = 7 cm. Find the area of the shaded region.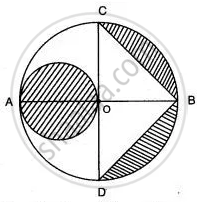
Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube. Find the edge of the cube so formed.
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
