Advertisements
Advertisements
Question
The length of the longest pole that can be kept in a room (12 m × 9 m ×8 m) is
Options
144 cm2
216 cm2
180 cm2
108 cm2
Solution
216 cm2
Let the edge of the cube be a cm.
Then, length of the diagonal `=sqrt(3"a")`
or,
`sqrt(3"a") = 6sqrt(3)`
⇒ a = 6 cm
Therefore, the total surface area of the cube = 6a2
`= (6xx6xx6) "cm"^3`
= 216 cm3
Therefore, the total surface area of the cube = 6a2
= (6 × 6 × 6 ) cm3
= 216 cm3
APPEARS IN
RELATED QUESTIONS
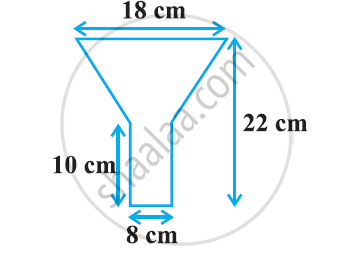
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of Rs 10 per 100 cm2. [Use π = 3.14]
In a cylindrical vessel of diameter 24 cm, filled up with sufficient quantity of water, a solid spherical ball of radius 6 cm is completely immersed. Find the increase in height of water level.
Height of a solid cylinder is 10 cm and diameter 8 cm. Two equal conical hole have been made from its both ends. If the diameter of the holes is 6 cm and height 4 cm, find (i) volume of the cylinder, (ii) volume of one conical hole, (iii) volume of the remaining solid.
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
The length of the longest pole that can be kept in a room (12 m × 9 m ×8 m) is
A metal cuboid of measures 16 cm × 11 cm × 10 cm was melted to make coins. How many coins were made, if the thickness and diameter of each coin was 2 mm and 2 cm respectively? (π = 3.14)
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
The radii of the top and bottom of a bucket of slant height 45cm are 28cm and 7 cm respectively. The curved surface area of the bucket is ______.
Match the column:
| (1) surface area of cuboid | (A) πr2h |
| (2) surface area of closed right cylinder | (B) 2πr(h + r) |
| (3) Total surface area of right cone | (C) πrl + πr2 |
| (4) Total surface area of hemisphere | (D) 3πr3 |
| (E) 3πr2 | |
| (F) 2[lb + bh + lh] |
