Advertisements
Advertisements
Question
A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5m and height 21m and the cone has a slant height 8m. Calculate total surface area and volume of the rocket?
Solution
Given radius of cylinder (a) = 2.5m
Height of cylinder (h) = 21m
Slant height of cylinder (l) = 8m
Curved surface area of cone(S1) = πrl
S1 = π(2.5)(8)cm2 ...........(1)
Curbed surface area of a cone`= 2pirh+pir^2`
`S_2=2pi(2.5)(21)+pi(2.5)^2cm^2` ...........(2)
∴Total curved surface area = (1) + (2)
S = S1 + S2
S = π(2.5)(8) + 2π(2.5)(21) + π(2.5)2
S = 62.831 + 329.86 + 19.63
S = 412.3m2
∴Total curved surface area = 412.3m2
Volume of a cone `=1/3pir^2h`
`V_1=1/3xxpi(2.5)^2h cm^3` .........(3)
Let ‘h’ be height of cone
`l^2=r^2+h^2`
⇒ `l^2-r^2=h^2`
⇒ `h=sqrt(l^2-r^2)`
⇒ `h=sqrt(8^2-25^2)`
⇒ h =23.685m
Subtracting ‘h’ value in(3)
Volume of a cone `(V_1)=1/3xxpi(2.5)^2(23.685) cm^2` ........(4)
Volume of a cylinder `(V_2)=pir^2h`
`=pi(2.5)^2 21m^3` ...........(5)
Total volume = (4) + (5)
V = V1 + V2
⇒ `V=1/3xxpi(2.5)^2(23.685)+pi(2.5)^2=1`
⇒ V = 461.84m2
Total volume (V) = 461.84m2
APPEARS IN
RELATED QUESTIONS
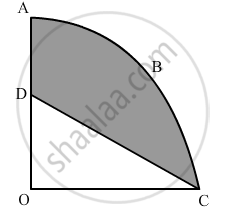
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
A tank of cylindrical shape has radius 2.8 m and its height 3.5 m. Complete the activity to find how many litres of water the tank will contain.
Capacity of water tank = Volume of cylindrical tank
= πr2h
Find the ratio of the volumes of a cylinder and a cone having equal radius and equal height.
(A)1 : 2 (B) 2 : 1 (C) 1 : 3 (D) 3 : 1
Lead spheres of diameter 6 cm are dropped into a cylindrical beaker containing some water and are fully submerged. If the diameter of the beaker is 18 cm and water rises by 40 cm. find the number of lead spheres dropped in the water.
A 5-m-wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of ₹25 per metre.
A shuttlecock used for playing badminton is a combination of

The radius of the base and the height of a solid right circular cylinder are in the ratio 2 : 3 and its volume is 1617 cm3. Find the total surface area of the cylinder.
The slant height of a bucket is 26 cm. The diameter of upper and lower circular ends are 36 cm and 16 cm. then height of bucket is ______.
A right circular cylinder of radius r cm and height h cm (h > 2r) just encloses a sphere of diameter ______.
A rectangular examination hall having seats for 500 candidates has to be built so as to allow 4 cubic metres of air and 0.5 square metres of floor area per candidate. If the length of hall be 25 m, find the height and breadth of the hall.
