Advertisements
Advertisements
प्रश्न
A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5m and height 21m and the cone has a slant height 8m. Calculate total surface area and volume of the rocket?
उत्तर
Given radius of cylinder (a) = 2.5m
Height of cylinder (h) = 21m
Slant height of cylinder (l) = 8m
Curved surface area of cone(S1) = πrl
S1 = π(2.5)(8)cm2 ...........(1)
Curbed surface area of a cone`= 2pirh+pir^2`
`S_2=2pi(2.5)(21)+pi(2.5)^2cm^2` ...........(2)
∴Total curved surface area = (1) + (2)
S = S1 + S2
S = π(2.5)(8) + 2π(2.5)(21) + π(2.5)2
S = 62.831 + 329.86 + 19.63
S = 412.3m2
∴Total curved surface area = 412.3m2
Volume of a cone `=1/3pir^2h`
`V_1=1/3xxpi(2.5)^2h cm^3` .........(3)
Let ‘h’ be height of cone
`l^2=r^2+h^2`
⇒ `l^2-r^2=h^2`
⇒ `h=sqrt(l^2-r^2)`
⇒ `h=sqrt(8^2-25^2)`
⇒ h =23.685m
Subtracting ‘h’ value in(3)
Volume of a cone `(V_1)=1/3xxpi(2.5)^2(23.685) cm^2` ........(4)
Volume of a cylinder `(V_2)=pir^2h`
`=pi(2.5)^2 21m^3` ...........(5)
Total volume = (4) + (5)
V = V1 + V2
⇒ `V=1/3xxpi(2.5)^2(23.685)+pi(2.5)^2=1`
⇒ V = 461.84m2
Total volume (V) = 461.84m2
APPEARS IN
संबंधित प्रश्न
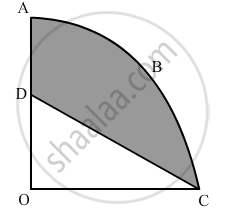
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
Find the volume of a sphere of diameter 6 cm.
A hemispherical bowl of internal radius 15 cm contains a liquid. The liquid is to be filled into cylindrical-shaped bottles of diameter 5 cm and height 6 cm. How many bottles are necessary to empty the bowl?
From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid. Also, find the total surface area of the remaining solid.
The volume of a sphere is 4851 cm3. Find its curved surface area.
The diameter of the base of a cylinder is 4 cm and its height is 14 cm. The volume of the cylinder is
Assertion (A)
If the radii of the circular ends of a bucket 24 cm high are 15 cm and 5 cm, respectively, then the surface area of the bucket is 545π cm2.
- Reason(R)
If the radii of the circular ends of the frustum of a cone are R and r, respectively, and its height is h, then its surface area is - Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
The volume of a sphere is 4851 cm3. Its diameter is ______.
A cube whose edge is 20 cm long, has circles on each of its faces painted black. What is the total area of the unpainted surface of the cube if the circles are of the largest possible areas?
Find the surface area of a sphere of radius 7 cm.
Solution :
The surface area of the sphere = 4πr2
= `4 xx 22/7 xx square^2`
= `4 xx 22/7 xx square`
= `square xx 7`
∴ The surface area of the sphere = `square` sq.cm.
