Advertisements
Advertisements
Question
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the figure is `(pir^2)/3 [3h - 2r]`.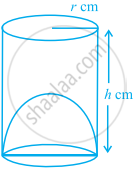
Options
True
False
Solution
This statement is True.
Explanation:
We know that,
Capacity of cylindrical vessel = πr2h cm3
And capacity of hemisphere = `2/3 pi"r"^3 "cm"`
From the figure,
Capacity of the cylindrical vessel
= `pi"r"^2"h" - 2/3 pi"r"^3`
= `1/3 pi"r"^2 [3"h" - 2"r"]`
APPEARS IN
RELATED QUESTIONS
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the volume of wood in the toy. `[\text{Use}pi 22/7]`
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of Rs 10 per 100 cm2. [Use π = 3.14]
Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m × 16 m × 11 m.
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
The surface areas of two spheres are in the ratio of 4 : 25. Find the ratio of their volumes.
Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
The circumference of the front wheel of a cart is 3 m long and that of the back wheel is 4 m long. What is the distance travelled by the cart, when the front wheel makes five more revolutions than the rear wheel?
The radius of a metallic sphere is 8 cm. It was melted to make a wire of diameter 6 mm. Find the length of the wire.
