Advertisements
Advertisements
Question
The radius of a metallic sphere is 8 cm. It was melted to make a wire of diameter 6 mm. Find the length of the wire.
Solution
The radius of a metallic sphere (r) = 8 cm
The diameter of a wire = 6 mm
∴ Its radius (r1) = 3 mm = `3/10` cm ......[∵ 1 cm = 10 mm]
Let h be the length.
Wire is created by melting a spherical.
∴ Volume of wire = Volume of sphere
∴ `πr_1^2h = 4/3 πr^3`
∴ `3/10 xx 3/10 xx h = 4/3 xx 8 xx 8 xx 8`
h = `(4 xx 8 xx 8 xx 8 xx 10 xx 10)/(3 xx 3 xx 3)`
h = `204800/27` = 7585.1851 cm
h = 75.85 m ......[∵ 1 m = 100 cm]
The length of the wire is 75.85 m.
APPEARS IN
RELATED QUESTIONS
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/12 cm, find the length of the wire.
A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
A right angled triangle whose sides are 3 cm, 4 cm and 5 cm is revolved about the sides containing the right angle in two days. Find the difference in columes of the two cones so formed. Also, find their curved surfaces.
A solid is in the shape of a frustum of a cone. The diameter of two circular ends are 60cm and 36cm and height is 9cm. find area of its whole surface and volume?
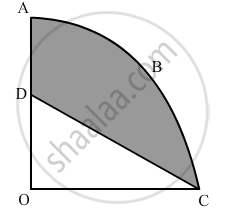
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
Water flows through a cylindrical pipe , whose inner radius is 1 cm , at the rate of 80 cm /sec in an empty cylindrical tank , the radius of whose base is 40 cm . What is the rise of water level in tank in half an hour ?
A metallic sphere 1 dm in diameter is beaten into a circular sheet of uniform thickness equal to 1 mm. Find the radius of the sheet.
A right circular cylinder and a right circular cone have equal bases and equal heights. If their curved surfaces are in the ratio 8 : 5, determine the ratio of the radius of the base to the height of either of them.
If the heights of two right circular cones are in the ratio 1 : 2 and the perimeters of their bases are in the ratio 3 : 4, what is the ratio of their volumes?
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
A vessel is in the form of a hemispherical bowl surmounted by a hollow cylinder. The diameter of the hemisphere is 21 cm and the total height of the vessel is 14.5 cm. Find its capacity.
A hemispherical tank, full of water, is emptied by a pipe at the rate of `25/7` litres per second. How much time will it take to empty half the tank if the diameter of the base of the tank is 3 m?
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
The volume of a sphere is 4851 cm3. Find its curved surface area.
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each hemispherical end is 7 cm, find the surface area of the solid.

In Figure 3, a decorative block is shown which is made of two solids, a cube, and a hemisphere. The base of the block is a cube with an edge 6 cm and the hemisphere fixed on the top has a diameter of 4⋅2 cm. Find
(a) the total surface area of the block.
(b) the volume of the block formed. `("Take" pi = 22/7)`
Tick the object which has more volume
A running track has 2 semicircular ends of radius 63 m and two straight lengths. The perimeter of the track is 1000 m. Find each straight length.
