Advertisements
Advertisements
Question
Water flows through a cylindrical pipe , whose inner radius is 1 cm , at the rate of 80 cm /sec in an empty cylindrical tank , the radius of whose base is 40 cm . What is the rise of water level in tank in half an hour ?
Solution
The inner radius of the cylindrical pipe r =1 cm.
Rate of flow of water = 80 cm/sec
volume of the water that flows through pipe in 1sec is
\[\pi r^2 \times 80 = 80\pi {cm}^3\]
volume of the water that flows through pipe in half an hour
\[80\pi \times 30 \times 60 = 144000\pi {cm}^3\]
radius of the base of the cylindrical tank is R = 40 cm
let the water level in the cylinderical tank after half an hour be h.
volume of the raised water = \[\pi \left( R \right)^2 h = \pi \left( 40 \right)^2 h\]
volume of the raised water in tank = volume of the water that flows through pipe
\[\Rightarrow \pi \left( 40 \right)^2 h = 144000\pi\]
\[ \Rightarrow h = \frac{144000}{1600} = 90 cm\]
Thus water level will rise by 90 cm in half an hour.
APPEARS IN
RELATED QUESTIONS
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
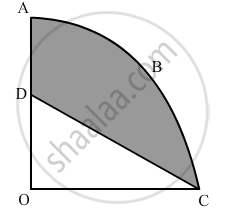
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
Water is flowing at the rate of 15 km/hour through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/hr. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired ?
A sphere of diameter 5 cm is dropped into a cylindrical vessel partly filled with water. The diameter of the base of the vessel is 10 cm. If the sphere is completely submerged, by how much will the level of water rise?
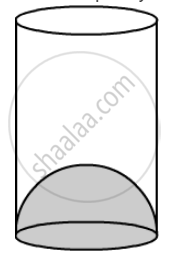
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
The dimensions of a metallic cuboid are 100cm× 80 cm× 64cm. It is melted and recast into a cube. Find the surface area of the cube.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total
surface area of the toy.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is ______.
The curved surface are of a cylinder is 1760 cm2 and its base radius is 14 cm. The height of the cylinder is
