Advertisements
Advertisements
Question
The dimensions of a metallic cuboid are 100cm× 80 cm× 64cm. It is melted and recast into a cube. Find the surface area of the cube.
Solution
Let the edge of cube be a.
As,
Volume of cube = Volume of cuboid
`rArr a^3 = 100xx80xx64`
`rArr a^3 = 100xx80xx64`
`rArr a = root(3)(512000)`
⇒ a =80 cm
Now, the surface area of the cube = 6a2
=6 ×80 ×80
= 38400 cm2
So, the surface area of the cube is 38400 cm2.
APPEARS IN
RELATED QUESTIONS
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
In a rain-water harvesting system, the rain-water from a roof of 22 m × 20 m drains into a cylindrical tank having diameter of base 2 m and height 3·5 m. If the tank is full, find the rainfall in cm. Write your views on water conservation.
The diameter and length of a roller is 120 cm and 84 cm respectively. To level the ground, 200 rotations of the roller are required. Find the expenditure to level the ground at the rate of Rs. 10 per sq.m.
The radius of the base of a right circular cone of semi-vertical angle α is r. Show that its volume is \[\frac{1}{3} \pi r^3\] cot α and curved surface area is πr2 cosec α.
The volumes of two cubes are in the ratio 8 : 27. Find the ratio of their surface areas.
Choose the correct answer of the following question:
A solid is hemispherical at the bottom and conical (of same radius) above it. If the surface areas of the two parts are equal, then the ratio of its radius and the slant height of the conical part is
Assertion (A)
If the volumes of two spheres are in the ratio 27 : 8, then their surface areas are in the ratio 3 : 2.
Reason (R)
Volume of a sphere `=4/3pi"R"^3`
Surface area of a sphere = 4πR2
Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the figure is `(pir^2)/3 [3h - 2r]`.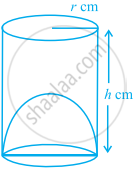
______ of a solid is the measurement of the space occupied by it.
If the length of the diagonal of a cube is `5sqrt(3)` cm, find the total surface area.
Length of the diagonal of the cube = `square`
So, `square` = `5sqrt(3)`
⇒ Side = `square`
Total surface area of cube = `square`
= `square` × `square` × `square`
= `square` cm2
Hence, the total surface area is `square`.
