Advertisements
Advertisements
Question
A cone of height 20 cm and radius of base 5 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the diameter of the sphere.
Solution
We have,
the base radius of the cone, r=5 cm and
the height of the cone, h = 20 cm
Let the radius of the sphere be R.
As,
Volume of sphere = Volume of cone
`rArr 4/3piR^3 = 1/3pir^2h`
`rArr R^3 = (pir^2hxx3)/(3xx4pi)`
`rArr R^3 = (r^2h)/4`
`rArr R^3 = (5xx5xx20)/4`
`rArr R^3 = 125`
`rArr R = root(3)(125)`
⇒ Diameter of the sphere = 2R= 2×5 = 10 cm
So, the diameter of the sphere is 10 cm.
APPEARS IN
RELATED QUESTIONS
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [use π=22/7]
A fez, the cap used by the Turks, is shaped like the frustum of a cone (see the figure given below). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material use for making it. [use π=22/7]

Derive the formula for the curved surface area and total surface area of the frustum of cone.
A 5 m wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of Rs 25 per metre ?\[[Use \pi = \frac{22}{7}]\]
A metallic bucket, open at the top, of height 24 cm is in the form of the frustum of a cone, the radii of whose lower and upper circular ends are 7 cm and 14 cm respectively. Find :
(i) the volume of water which can completely fill the bucket.
(ii) the area of the metal sheet used to make the bucket.
[Use π =\[\frac{22}{7}\]
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
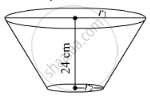
A bucket of height 24 cm is in the form of frustum of a cone whose circular ends are of diameter 28 cm and 42 cm. Find the cost of milk at the rate of ₹30 per litre, which the bucket can hold.
The circular ends of a bucket are of radii 35 cm and 14 cm and the height of the bucket is 40 cm. Its volume is
An oil funnel of the tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion by 8 cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.
