Advertisements
Advertisements
Question
A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/12 cm, find the length of the wire.
Solution
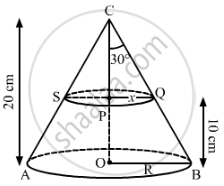

Let ACB be the cone whose vertical angle ∠ACB = 60°. Let R and x be the radii of the lower and upper end of the frustum.
Here, height of the cone, OC = 20 cm = H
Height CP = h = 10 cm
Let us consider P as the mid-point of OC.
After cutting the cone into two parts through P,
OP = 20/2=10 cm
Also, ∠ACO and ∠OCB = (1/2)×60°=30°
After cutting cone CQS from cone CBA, the remaining solid obtained is a frustum.
Now, in triangle CPQ:
`tan30^@=x/10`
`⇒1/sqrt3=x/10`
`⇒x=10/sqrt3cm`
In triangle COB:
`tan30^@=R/"CO"`
`⇒1/sqrt3=R/20`
`⇒R=20/sqrt3 cm`
Volume of the frustum, V=1/3π(R2H − x2h)
`⇒V=1/3π((20/sqrt3)^2⋅20−(10/sqrt3)^2⋅10)`
`=1/3π(8000/3−1000/3)`
`= 1/3π(7000/3)`
`=1/9π×7000`
`=7000/9π`
The volumes of the frustum and the wire formed are equal.
`πxx(1/24)^2xxl=7000/9π [Volume of wire =πr2h]`
`⇒l=7000/9xx24xx24`
⇒l=448000 cm=4480 m
Hence, the length of the wire is 4480 m.
APPEARS IN
RELATED QUESTIONS
A solid sphere of diameter 6 cm is dropped in a right circular cylindrical vessel partly filled with water. The diameter of the cylindrical vessel is 12 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel?
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
A solid metallic spherical ball of diameter 6 cm is melted and recast into a cone with diameter of the base as 12 cm. The height of the cone is
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
The surface areas of a sphere and a cube are equal. Find the ratio of their volumes.

In Figure 3, a decorative block is shown which is made of two solids, a cube, and a hemisphere. The base of the block is a cube with an edge 6 cm and the hemisphere fixed on the top has a diameter of 4⋅2 cm. Find
(a) the total surface area of the block.
(b) the volume of the block formed. `("Take" pi = 22/7)`
The volume of a sphere is 4851 cm3. Its diameter is ______.
A cube whose edge is 20 cm long, has circles on each of its faces painted black. What is the total area of the unpainted surface of the cube if the circles are of the largest possible areas?
Volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
