Advertisements
Advertisements
Question
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the volume of wood in the toy. `[\text{Use}pi 22/7]`
Solution
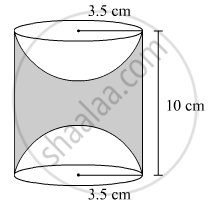
Height of the cylinder, h = 10 cm
Radius of the cylinder = Radius of each hemisphere = r = 3.5 cm
Volume of wood in the toy = Volume of the cylinder − 2 × Volume of each hemisphere
`=pir^2h-2xx2/3pir^2`
`=22/7xx(3.5cm)^2xx10cm-4/3xx22/7xx(3.5cm)^3`
`=385cm^3-539/3cm^3`
`=616/3cm^3`
`=205.33cm^3`(Approx)
Thus, the volume of the wood in the toy is approximately 205.33 cm3.
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of radius 7 cm.
Radius of a sphere is 14 cm. Find the surface area of the sphere.
Water flows at the rate of 10 m / minute through a cylindrical pipe 5 mm in diameter . How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm.
A spherical ball of iron has been melted and made into smaller balls. If the radius of each smaller ball is one-fourth of the radius of the original one, how many such balls can be made?
The diameters of two circular ends of the bucket are 44 cm and 24 cm . The height of the bucket is 35 cm . The capacity of the bucket is
If the radii of the ends of a bucket are 5 cm and 15 cm and it is 24 cm high, then its surface area is
The slant height of a bucket is 26 cm. The diameter of upper and lower circular ends are 36 cm and 16 cm. then height of bucket is ______.
A cube whose edge is 20 cm long, has circles on each of its faces painted black. What is the total area of the unpainted surface of the cube if the circles are of the largest possible areas?
Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
The length, breadth and height of a cuboidal reservoir is 7 m, 6 m and 15 m respectively. 8400 L of water is pumped out from the reservoir. Find the fall in the water level in the reservoir.
