Advertisements
Advertisements
Question
If the radii of the ends of a bucket are 5 cm and 15 cm and it is 24 cm high, then its surface area is
Options
1815.3 cm2
1711.3 cm2
2025.3cm2
2360 cm2
Solution
1711.3 cm2
Let R and r be the radii of the top and base of the bucket, respectively, and let h and l be its height and slant height.
Then,
R = 15 cm , r = 5 cm , h = cm
`"l"=sqrt("h"^2 + ("R" - r)^2)`
`=sqrt((24)^2 + (15 - 5)^2)
`=sqrt(576+100)`
`=sqrt(676)`
= 26 cm
surface area of the bucket` = pi["r"^2 + l ("R" + "r")]`
`= 3.14xx(5^2 + 26(15+5))`
`= (3.14xx(26xx20+25)) "cm"^2`
`= 1711.3 "cm"^2`
APPEARS IN
RELATED QUESTIONS
The `3/4` th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
A right angled triangle whose sides are 3 cm, 4 cm and 5 cm is revolved about the sides containing the right angle in two days. Find the difference in columes of the two cones so formed. Also, find their curved surfaces.
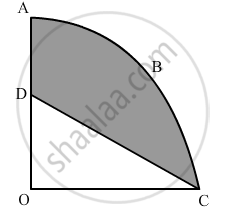
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
A tent is in the shape of a right circular cylinder up to a height of 3 m and conical above it. The total height of the tent is 13.5 m and the radius of its base is 14 m. Find the cost of cloth required to make the tent at the rate of Rs 80 per square metre.
Choose the correct answer of the following question:
The surface areas of two spheres are in the ratio 16 : 9. The ratio of their volumes is
If each edge of a cube is increased by 50%, the percentage increase in the surface area is
The ratio between the volume of two spheres is 8 : 27. What is the ratio between their surface areas?
______ of a solid is the measurement of the space occupied by it.
