Advertisements
Advertisements
Question
Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
Solution
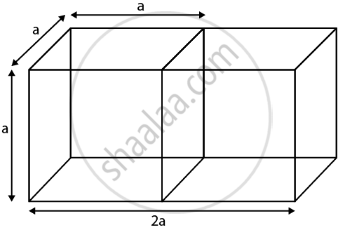
Let the side of one cube = a
Surfaces area of resulting cuboid = 2(Total surface area of a cube) – 2(area of single surface)
We know that,
Total surface area of cube = 6a2, where a = side of cube
⇒ Surfaces area of resulting cuboid = 2(6a2) – 2(a2) = 10a2
Also,
According to the question,
Volume of cube = 64 cm3
Volume of cube = a3
64 = a3
a = 4 cm
Therefore, surface area of resulting cuboid = 10a2 = 10(4)2 = 160 cm2
APPEARS IN
RELATED QUESTIONS
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3 `5/9` cm. Find the diameter of the cylindrical vessel.
Find the volume of a sphere of diameter 6 cm.
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
In a corner of a rectangular field with dimensions 35m × 22 m, a well with 14 m inside diameter is dug 8 m deep. The earth dug out is spread evenly over the remaining part of the field. Find the rise in the level of the field.
If the surface area of a sphere is 616 cm2, its diameter (in cm) is ______. (Taking π = `22/7`)
The sum of length, breadth and height of a cuboid is 19 cm and its diagonal is `5sqrt(5)` cm. Its surface area is
The surface area of a sphere is 154 cm2. The volume of the sphere is
Assertion (A)
The outer surface of a hemisphere of radius 7 cm is to be painted. The total cost of painting at Rs 5 per cm2 is Rs 2300.
Reason (R)
The total surface area of a hemisphere is 3π r2.
- Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
Match the column:
| (1) surface area of cuboid | (A) πr2h |
| (2) surface area of closed right cylinder | (B) 2πr(h + r) |
| (3) Total surface area of right cone | (C) πrl + πr2 |
| (4) Total surface area of hemisphere | (D) 3πr3 |
| (E) 3πr2 | |
| (F) 2[lb + bh + lh] |
The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. The curved surface area of the bucket is ______.
