Advertisements
Advertisements
प्रश्न
Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
उत्तर
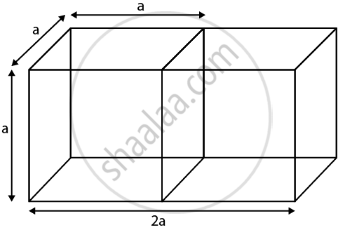
Let the side of one cube = a
Surfaces area of resulting cuboid = 2(Total surface area of a cube) – 2(area of single surface)
We know that,
Total surface area of cube = 6a2, where a = side of cube
⇒ Surfaces area of resulting cuboid = 2(6a2) – 2(a2) = 10a2
Also,
According to the question,
Volume of cube = 64 cm3
Volume of cube = a3
64 = a3
a = 4 cm
Therefore, surface area of resulting cuboid = 10a2 = 10(4)2 = 160 cm2
APPEARS IN
संबंधित प्रश्न
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
A sphere and a cube have equal surface areas. What is the ratio of the volume of the sphere to that of the cube?
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
A sphere of radius 6 cm is dropped into a cylindrical vessel partly filled with water. The radius of the vessel is 8 cm. If the sphere is submerged completely, then the surface of the water rises by
The volume of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is
The interior of a building is in the form of a right circular cylinder of diameter 4.2 m and height 4 m surmounted by a cone of same diameter.
The height of the cone is 2.8 m. Find the outer surface area of the building.
Assertion (A)
If the radii of the circular ends of a bucket 24 cm high are 15 cm and 5 cm, respectively, then the surface area of the bucket is 545π cm2.
- Reason(R)
If the radii of the circular ends of the frustum of a cone are R and r, respectively, and its height is h, then its surface area is - Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
A sphere and a cube have equal surface areas. The ratio of the volume of the sphere to that of cube is ______.
There is a circular pond and a footpath runs along its boundary. A person walks around it, exactly once keeping close to the edge. If his step is 66 cm long and he takes exactly 400 steps to go around the pond, find the diameter of the pond.
If the length of the diagonal of a cube is `5sqrt(3)` cm, find the total surface area.
Length of the diagonal of the cube = `square`
So, `square` = `5sqrt(3)`
⇒ Side = `square`
Total surface area of cube = `square`
= `square` × `square` × `square`
= `square` cm2
Hence, the total surface area is `square`.
