Advertisements
Advertisements
प्रश्न
A sphere of radius 6 cm is dropped into a cylindrical vessel partly filled with water. The radius of the vessel is 8 cm. If the sphere is submerged completely, then the surface of the water rises by
विकल्प
4.5 cm
3
4 cm
2 cm
उत्तर
Radius of the sphere = 6 cm.
Volume of the sphere
`=4/3pir^3`
`=4/3 pi xx 6 xx 6 xx 6`
and
Radius of the cylinder = 8 cm
Volume of the cylinder
`=pir^2h`
`=pi xx 8 xx 8 xx h`
Therefore,
Volume of the sphere = volume of the cylinder
`4/3pi(6)^3 = pi(8)^2 h`
or
`h = (4 xx 72)/64 = 4.5 cm`
APPEARS IN
संबंधित प्रश्न
In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park. Write your views on recycling of water.
The capacity of a certain cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its height and length are 10 m and 2.5 m respectively.
A cubic cm of gold is drawn into a wire 0.1 mm in diameter, find the length of the wire.
The surface area of a sphere is 616 cm2 . Find its radius.
A 5-m-wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of ₹25 per metre.
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 98 cm and the diameter of each of its hemispherical ends is 28 cm, find the cost of polishing the surface of the solid at the rate of 15 paise per sq cm.
Three cubes of iron whose edges are 6 cm, 8 cm and 10 cm, respectively are melted and formed into a single cube. Find the edge of the new cube formed.
A shuttlecock used for playing badminton is a combination of

The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the figure is `(pir^2)/3 [3h - 2r]`.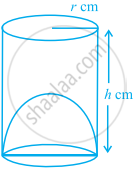
The curved surface area of a right circular cone is 12320 cm2. If the radius of its base is 56 cm, then find its height.
