Advertisements
Advertisements
प्रश्न
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it to a width of 4 m to form an embankment. Find the height of the embankment.
उत्तर
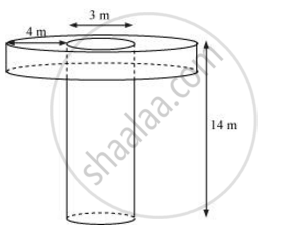
The shape of the well will be cylindrical.
Depth (h1) of well = 14 m
Radius (r1) of the circular end of well = 3/2 m
Width of embankment = 4 m
From the figure, it can be observed that our embankment will be in a cylindrical shape having outer radius (r2) as 4 + 3/2 =11/2 m and inner radius (r1) as 3/2 m
Let the height of embankment be h2.
Volume of soil dug from well = Volume of earth used to form embankment
`pixxr_1^2xxh_1 = pixx(r_2^2-r_1^2)xxh_2`
`pixx(3/2)^2xx 14 =pixx[(11/2)^2-(3/2)^2]xxh`
`9/4xx14 = 112/4 xx h`
h = 9/8 = 1.125 m
Therefore, the height of the embankment will be 1.125 m.
संबंधित प्रश्न
In a rain-water harvesting system, the rain-water from a roof of 22 m × 20 m drains into a cylindrical tank having diameter of base 2 m and height 3·5 m. If the tank is full, find the rainfall in cm. Write your views on water conservation.
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
The capacity of a certain cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its height and length are 10 m and 2.5 m respectively.
A building is in the form of a cylinder surrounded by a hemispherical dome. The base diameter of the dome is equal to \[\frac{2}{3}\] of the total height of the building . Find the height of the building , if it contains \[67\frac{1}{21} m^3\].
Find the weight of a hollow sphere of metal having internal and external diameters as 20 cm and 22 cm, respectively if 1m3 of metal weighs 21g.
A sphere and a cube have equal surface areas. What is the ratio of the volume of the sphere to that of the cube?
What is the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height?
The ratio of the total surface area to the lateral surface area of a cylinder with base radius 80 cm and height 20 cm is
The radius of the base of a cone is 5 cm and its height is 12 cm. Its curved surface area is
If R is the radius of the base of the hat, then the total outer surface area of the hat is ______.

