Advertisements
Advertisements
प्रश्न
What is the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height?
उत्तर
Given that the diameter and the height of the cylinder, cone and sphere are the same.
The volume of cylinder, `v_1 = pir_1^2 h_1`= \[\pi \left( \frac{d}{2} \right)^2 d\]
The volume of cone, = `v_2 = 1/3pir_2^2 h_2`
\[\frac{1}{3}\pi \left( \frac{d}{2} \right)^2 d\]
And the volume of sphere,= `v_3 = 4/3pir_3^3`
\[\frac{4}{3}\pi \left( \frac{d}{2} \right)^3\]
Therefore,
The ratio of their volumes,
\[v_1 = v_2 = v_3 \]
\[ \Rightarrow \pi \left( \frac{d}{2} \right)^2 d = \frac{1}{3}\pi \left( \frac{d}{2} \right)^2 d = \frac{4}{3}\pi \left( \frac{d}{2} \right)^3 \]
\[ \Rightarrow 3: 1: 2\]
Hence, the ratio is 3 : 1 : 2
APPEARS IN
संबंधित प्रश्न
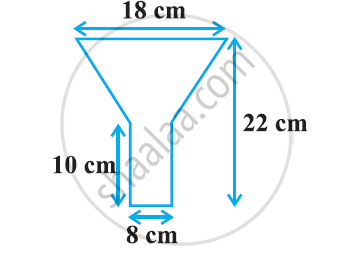
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).
In a rectangular park of dimensions 50 m × 40 m, a rectangular pond is constructed so that the area of grass strip of uniform width surrounding the pond would be 1184 m2. Find the length and breadth of the pond ?
A factory manufactures 120,000 pencils daily . The pencil are cylindrical in shape each of length 25 cm and circumference of base as 1.5 cm . Determine the cost of colouring the curved surfaces of the pencils manufactured in one day at ₹0.05 per dm2.
The radius of the base of a right circular cone of semi-vertical angle α is r. Show that its volume is \[\frac{1}{3} \pi r^3\] cot α and curved surface area is πr2 cosec α.
The interior of a building is in the form of a cylinder of base radius 12 m and height 3.5 m, surmounted by a cone of equal base and slant height 12.5 m. Find the internal curved surface area and the capacity of the building.
The surface area of a sphere is 616 cm2 . Find its radius.
The surface areas of two spheres are in the ratio of 4 : 25. Find the ratio of their volumes.
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.

In the above figure, a sphere is placed in a cylinder. It touches the top, bottom and curved surface of the cylinder. If the radius of the base of the cylinder is ‘r’, write the answer to the following questions.
a. What is the height of the cylinder in terms of ‘r’?
b. What is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
c. What is the ratio of volumes of the cylinder and of the sphere?
A rectangular examination hall having seats for 500 candidates has to be built so as to allow 4 cubic metres of air and 0.5 square metres of floor area per candidate. If the length of hall be 25 m, find the height and breadth of the hall.
