Advertisements
Advertisements
प्रश्न
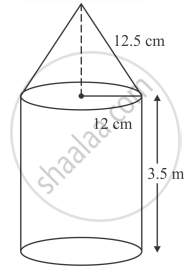
The interior of a building is in the form of a cylinder of base radius 12 m and height 3.5 m, surmounted by a cone of equal base and slant height 12.5 m. Find the internal curved surface area and the capacity of the building.
उत्तर
Height of the cone
`=sqrt((12.5)^2 - (12)^2)`
`=sqrt(12.25)`
`= 3.5m`
Capacity (volume) of cone
`=1/3 pir^2h`
`=1/3 xx 22/7 xx 12 xx 3.5`
`=528 m^3`
Capacity (volume) of cylinder
`=pir^2 h`
`=22/7 xx 12xx 12 xx 3.5`
`=1584 m^3`
Therefore,
Total capacity of building
`= 1584 + 528`
`=2112 m^3`
Internal curved surface area of the building
`=2pirh + pirl`
`= pir(2h+l)`
`=22/7 xx 12 (2 xx 3.5 + 12.5)`
`=22/7 xx 12 xx 19.5`
`=735.43m^2`
APPEARS IN
संबंधित प्रश्न
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
The dimensions of a metallic cuboid are 100cm× 80 cm× 64cm. It is melted and recast into a cube. Find the surface area of the cube.
A solid metallic sphere of diameter 8 cm is melted and drawn into a cylindrical wire of uniform width. If the length of the wire is 12 m, then find its width.
A sphere of diameter 18 cm is dropped into a cylindrical vessel of diameter 36 cm, partly filled with water. If the sphere is completely submerged, then the water level rises by ______.
Assertion (A)
The outer surface of a hemisphere of radius 7 cm is to be painted. The total cost of painting at Rs 5 per cm2 is Rs 2300.
Reason (R)
The total surface area of a hemisphere is 3π r2.
- Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
The surface area of a sphere is 616 cm2. Its radius is ______.
A cube whose edge is 20 cm long, has circles on each of its faces painted black. What is the total area of the unpainted surface of the cube if the circles are of the largest possible areas?
The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. The curved surface area of the bucket is ______.
