Advertisements
Advertisements
प्रश्न
The interior of a building is in the form of a cylinder of base radius 12 m and height 3.5 m, surmounted by a cone of equal base and slant height 12.5 m. Find the internal curved surface area and the capacity of the building.
उत्तर
Height of the cone
`=sqrt((12.5)^2 - (12)^2)`
`=sqrt(12.25)`
`= 3.5m`
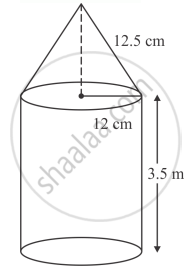
Capacity (volume) of cone
`=1/3 pir^2h`
`=1/3 xx 22/7 xx 12 xx 3.5`
`=528 m^3`
Capacity (volume) of cylinder
`=pir^2 h`
`=22/7 xx 12xx 12 xx 3.5`
`=1584 m^3`
Therefore,
Total capacity of building
`= 1584 + 528`
`=2112 m^3`
Internal curved surface area of the building
`=2pirh + pirl`
`= pir(2h+l)`
`=22/7 xx 12 (2 xx 3.5 + 12.5)`
`=22/7 xx 12 xx 19.5`
`=735.43m^2`
APPEARS IN
संबंधित प्रश्न
A spherical ball of iron has been melted and made into smaller balls. If the radius of each smaller ball is one-fourth of the radius of the original one, how many such balls can be made?
Find the weight of a hollow sphere of metal having internal and external diameters as 20 cm and 22 cm, respectively if 1m3 of metal weighs 21g.
A cylindrical vessel 32 cm high and 18 cm as the radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, the radius of its base is
The curved surface area of a cylinder is 264 m2 and its volume is 924 m3. The ratio of its diameter to its height is
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
Two cubes, each of volume 64 cm3, are joined end to end. Find the total surface area of the resulting cuboid.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3 . the radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it.
The surface area of a sphere is 616 cm2. Its radius is ______.
The shape of a gilli, in the gilli-danda game (see Fig.), is a combination of ______.

Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
