Advertisements
Advertisements
प्रश्न
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gram mass approximately. (Use : π = 355/115)
उत्तर
Volume of cylinder
`=pir^2 h`
`=22/7 xx 6 xx 6 xx 110`
`=12445. 714 cm^3`
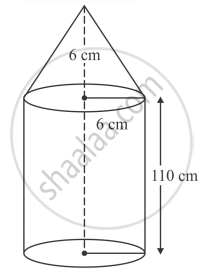
Volume of cone
`=1/3pir^2h`
`=1/3 xx 22/7 xx 6 xx 6 xx 9`
`=339.429 cm^3`
Therefore,
Total volume
`=12445.714 +339.429`
`=12785 . 123 cm^3`
Therefore,
Mass of the pole
` =8 xx 12785.143 cm^3`
`= 102281.12 cm`
`= 102.28kg`
APPEARS IN
संबंधित प्रश्न
A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm3 of water.The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of the metal sheet used in its making. (Use 𝜋 = 3.14).
A building is in the form of a cylinder surmounted by a hemi-spherical vaulted dome and contains \[41\frac{19}{21} m^3\] of air. If the internal diameter of dome is equal to its total height above the floor , find the height of the building ?
Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
The radii of the ends of a bucket of height 24 cm are 15 cm and 5 cm. Find its capacity. (Take π = 22/7)
The radii of two cylinders are in the ratio 3 : 5 and their heights are in the ratio 2 : 3. What is the ratio of their curved surface areas?
Two cones have their heights in the ratio 1 : 3 and radii 3 : 1. What is the ratio of their volumes?
A vessel is in the form of a hemispherical bowl surmounted by a hollow cylinder. The diameter of the hemisphere is 21 cm and the total height of the vessel is 14.5 cm. Find its capacity.
From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid. Also, find the total surface area of the remaining solid.
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, then find the total area of the canvas required.
In a right circular cone, if the perpendicular height is 12 cm and the radius is 5 cm, then find its slant height.
