Advertisements
Advertisements
प्रश्न
A tent of height 8.25 m is in the form of a right circular cylinder with diameter of base 30 m and height 5.5 m, surmounted by a right circular cone of the same base. Find the cost of the canvas of the tent at the rate of Rs 45 per m2.
उत्तर
`l = sqrt((2.75)^2) + (15)^2`
`l = sqrt(232.5625)`
`= 15 .25`
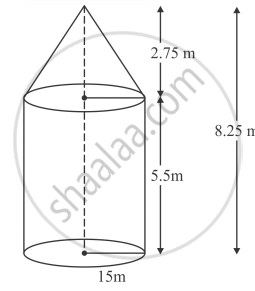
Total surface area of the tent
`=2 pirh + pirl`
`=pir(2h + l)`
`=22/7 xx 15[2 xx 5 -5 + 15.25]`
`= (330 xx 26.25)/7`
`=1237.5`
Therefore,
Cost of the canvas of the tent
`=1237.5 xx 45`
`= "Rs . 55687.50"`
APPEARS IN
संबंधित प्रश्न
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
A building is in the form of a cylinder surmounted by a hemi-spherical vaulted dome and contains \[41\frac{19}{21} m^3\] of air. If the internal diameter of dome is equal to its total height above the floor , find the height of the building ?
The interior of a building is in the form of a cylinder of base radius 12 m and height 3.5 m, surmounted by a cone of equal base and slant height 12.5 m. Find the internal curved surface area and the capacity of the building.
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
The volume of a cube is 2744 cm2. Its surface area is
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If its volume is 1617 cm3, the total surface area of the cylinder is
Assertion (A)
If the radii of the circular ends of a bucket 24 cm high are 15 cm and 5 cm, respectively, then the surface area of the bucket is 545π cm2.
- Reason(R)
If the radii of the circular ends of the frustum of a cone are R and r, respectively, and its height is h, then its surface area is - Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. Find the curved surface area of the bucket.
Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
Find the surface area of a sphere of radius 7 cm.
Solution :
The surface area of the sphere = 4πr2
= `4 xx 22/7 xx square^2`
= `4 xx 22/7 xx square`
= `square xx 7`
∴ The surface area of the sphere = `square` sq.cm.
