Advertisements
Advertisements
प्रश्न
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
उत्तर
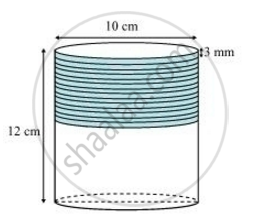
It can be observed that 1 round of wire will cover 3 mm height of cylinder.
Number of rounds = Height of cylinder/Diameter of wire
= 12/0.3 = 40 rounds
Length of wire required in 1 round = Circumference of base of cylinder
= 2πr = 2π × 5 = 10π
Length of wire in 40 rounds = 40 × 10π
`= (400xx22)/7 = 8800/7`
= 1257.14 cm = 12.57 m
Radius of wire = 0.3/2 = 0.15 cm
Volume of wire = Area of cross-section of wire × Length of wire
= π(0.15)2 × 1257.14
= 88.898 cm3
Mass = Volume × Density
= 88.898 × 8.88
= 789.41 gm
APPEARS IN
संबंधित प्रश्न
A metallic sphere 1 dm in diameter is beaten into a circular sheet of uniform thickness equal to 1 mm. Find the radius of the sheet.
A metallic sphere of radius 10.5 cm is melted and thus recast into small cones, each of radius 3.5 cm and height 3 cm. Find how many cones are obtained.
An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cubic cm of iron weighs 7.5 gm.
The dimensions of a metallic cuboid are 100cm× 80 cm× 64cm. It is melted and recast into a cube. Find the surface area of the cube.
The radius of the base of a cone is 5 cm and its height is 12 cm. Its curved surface area is
Assertion (A)
If the radii of the circular ends of a bucket 24 cm high are 15 cm and 5 cm, respectively, then the surface area of the bucket is 545π cm2.
- Reason(R)
If the radii of the circular ends of the frustum of a cone are R and r, respectively, and its height is h, then its surface area is - Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, then find the total area of the canvas required.
Arrange the given objects according to their volume
The internal and external radii of a spherical shell are 3cm and 5cm respectively. It is melted and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder. Also find the total surface area of the cylinder. (Take `pi = 22/7`)
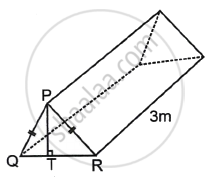
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent