Question

A right triangle whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate.)

Answer 1

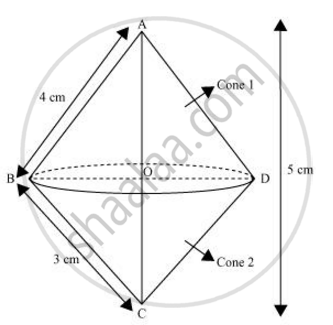
The double cone so formed by revolving this right-angled triangle ABC about its hypotenuse is shown in the figure.

Hypotenuse AC = `sqrt(3^2+4^2)`

=`sqrt25` = 5 cm

Area of ΔABC = 1/2 x AB x AC

`1/2xx AC xx OB = 1/2xx4xx3`

`1/2xx5xxOB = 6`

OB = 12/5 = 2.4 cm

Volume of double cone = Volume of cone 1 + Volume of cone 2

`=1/3 pir^2h_1 + 1/3 pir^2h_2`

`=1/3pir^2(h_1+h_2)=1/3pir^2(OA+OC)`

`=1/3xx3.14xx(2.4)^2(5)`

=30.14 cm³

Surface area of double cone = Surface area of cone 1 + Surface area of cone 2

= πrl₁ + πrl₂

= πr[4+3] = 3.14 x 2.4 x 7

= 52.75 cm²