Advertisements
Advertisements
Question
A right triangle whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate.)
Solution
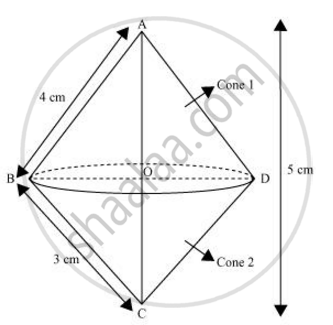
The double cone so formed by revolving this right-angled triangle ABC about its hypotenuse is shown in the figure.
Hypotenuse AC = `sqrt(3^2+4^2)`
=`sqrt25` = 5 cm
Area of ΔABC = 1/2 x AB x AC
`1/2xx AC xx OB = 1/2xx4xx3`
`1/2xx5xxOB = 6`
OB = 12/5 = 2.4 cm
Volume of double cone = Volume of cone 1 + Volume of cone 2
`=1/3 pir^2h_1 + 1/3 pir^2h_2`
`=1/3pir^2(h_1+h_2)=1/3pir^2(OA+OC)`
`=1/3xx3.14xx(2.4)^2(5)`
=30.14 cm3
Surface area of double cone = Surface area of cone 1 + Surface area of cone 2
= πrl1 + πrl2
= πr[4+3] = 3.14 x 2.4 x 7
= 52.75 cm2
APPEARS IN
RELATED QUESTIONS
A well of diameter 4 m is dug 21 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 3 m to form an embankment. Find the height of the embankment.
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
Find the total surface area of a cylinder if the radius of its base is 5 cm and height is 40 cm.
Water flows at the rate of 10 m / minute through a cylindrical pipe 5 mm in diameter . How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm.
A metallic sphere 1 dm in diameter is beaten into a circular sheet of uniform thickness equal to 1 mm. Find the radius of the sheet.
The radii of the circular ends of a bucket of height 15 cm are 14 cm and r cm (r < 14). If the volume of bucket is 5390 cm3, then find the value of r.
The interior of a building is in the form of a right circular cylinder of diameter 4.2 m and height 4 m surmounted by a cone of same diameter.
The height of the cone is 2.8 m. Find the outer surface area of the building.
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
The diameter of a cylinder is 28 cm and its height is 20 cm. The total surface area of the cylinder is
A circle of maximum possible size is cut from a square sheet of board. Subsequently, a square of maximum possible size is cut from the resultant circle. What will be the area of the final square?
