Advertisements
Advertisements
Question
A circle of maximum possible size is cut from a square sheet of board. Subsequently, a square of maximum possible size is cut from the resultant circle. What will be the area of the final square?
Options
`3/4` of original square.
`1/2` of original square.
`1/4` of original square.
`2/3` of original square.
Solution
`bb(1/2 "of original square")`.
Explanation:
Let a be the side of a square sheet.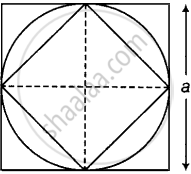
Then, area of bigger square sheet = a2 ...(i)
Now, we make the circle of maximum possible size from it.
Then, the radius of circle = `a/2` ...(ii)
So, its diameter (d) = `2 * a/2 = a`
Now, any square in a circle of maximum size will have the length of diagonal equal to the diameter of circle.
i.e Diagonal of square made inside the circle = a
So, the side of this square = `a/sqrt(2)` ...[∵ Diagonal = side `sqrt(2)`]
∴ Area of this square = `a^2/2` ...(iii)
From equations (i) and (iii),
Area of final square is `1/2` of original square.
APPEARS IN
RELATED QUESTIONS
A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. Determine the internal diameter of the shell.
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/hr. How much area will it irrigate in 10 minutes if 8 cm of standing water is needed for irrigation?
The volume of a cube is 2744 cm2. Its surface area is
If each edge of a cube is increased by 50%, the percentage increase in the surface area is
The area of the base of a right circular cone is 154 cm2 and its height is 14 cm. Its curved surface area is
In a right circular cone, if the perpendicular height is 12 cm and the radius is 5 cm, then find its slant height.
Match the column:
| (1) surface area of cuboid | (A) πr2h |
| (2) surface area of closed right cylinder | (B) 2πr(h + r) |
| (3) Total surface area of right cone | (C) πrl + πr2 |
| (4) Total surface area of hemisphere | (D) 3πr3 |
| (E) 3πr2 | |
| (F) 2[lb + bh + lh] |
The capacity of a closed cylindrical vessel of height 1 m is 15.4 L. How many square metres of metal sheet would be needed to make it?
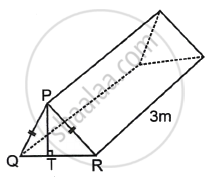
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent