Advertisements
Advertisements
Question
The interior of a building is in the form of a right circular cylinder of diameter 4.2 m and height 4 m surmounted by a cone of same diameter.
The height of the cone is 2.8 m. Find the outer surface area of the building.
Solution

We have,
Radius of the cylinder = Radius of the cone `= "r" = 4.2/2 = 2.1 "m",`
`"Height of the cylinder", "H" = 4 "m"` and
Height of the cone, h = 2.8 m
Also,
The slant height of the cone, `"l" =sqrt("r"^2+"h"^2)`
`=sqrt(2.1^2 + 2.8^2)`
`=sqrt(4.41+7.84)`
`=sqrt(12.25)`
`=3.5 "m"`
Now,
The outer surface area of the building = CSA 0f the cylinder + CSA of the cone
`=2pi"rH" + pi"rl"`
`=pir(2"H"+"l")`
`=22/7xx2.1xx(2xx4+3.5)`
`=6.6xx11.5`
= 75.9 m2
So, the outer surface area of the building is 75.9 m2 .
APPEARS IN
RELATED QUESTIONS
In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 7280 km2, show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
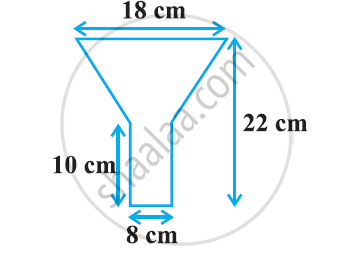
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).
A building is in the form of a cylinder surrounded by a hemispherical dome. The base diameter of the dome is equal to \[\frac{2}{3}\] of the total height of the building . Find the height of the building , if it contains \[67\frac{1}{21} m^3\].
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
The diameter of a sphere is 6 cm. It is melted and drawn in to a wire of diameter 2 mm. The length of the wire is
The dimensions of a metallic cuboid are 100cm× 80 cm× 64cm. It is melted and recast into a cube. Find the surface area of the cube.
A river 1.5 m deep and 36 m wide is flowing at the rate of 3.5 km/hr. Find the amount of water (in cubic metres) that runs into the sea per minute.
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, then find the total area of the canvas required.
A metal cuboid of measures 16 cm × 11 cm × 10 cm was melted to make coins. How many coins were made, if the thickness and diameter of each coin was 2 mm and 2 cm respectively? (π = 3.14)
______ of a solid is the measurement of the space occupied by it.
