Advertisements
Advertisements
Question
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
Solution
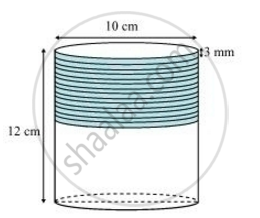
It can be observed that 1 round of wire will cover 3 mm height of cylinder.
Number of rounds = Height of cylinder/Diameter of wire
= 12/0.3 = 40 rounds
Length of wire required in 1 round = Circumference of base of cylinder
= 2πr = 2π × 5 = 10π
Length of wire in 40 rounds = 40 × 10π
`= (400xx22)/7 = 8800/7`
= 1257.14 cm = 12.57 m
Radius of wire = 0.3/2 = 0.15 cm
Volume of wire = Area of cross-section of wire × Length of wire
= π(0.15)2 × 1257.14
= 88.898 cm3
Mass = Volume × Density
= 88.898 × 8.88
= 789.41 gm
APPEARS IN
RELATED QUESTIONS
A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/hr. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired ?
Two cylindrical vessels are filled with oil. Their radii are 15 cm, 12 cm and heights 20 cm, 16 cm respectively. Find the radius of a cylindrical vessel 21 cm in height, which will just contain the oil of the two given vessels.
Find the weight of a hollow sphere of metal having internal and external diameters as 20 cm and 22 cm, respectively if 1m3 of metal weighs 21g.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
If the radii of the circular ends of a bucket 28 cm high, are 28 cm and 7 cm, then find its capacity and total surface area.
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
The surface area of a sphere is 154 cm2. The volume of the sphere is
In a right circular cone, if the perpendicular height is 12 cm and the radius is 5 cm, then find its slant height.
The dimensions of a metallic cuboid are 44 cm × 42 cm × 21 cm. it is molten and recast into a sphere. Find the surface area of the sphere.
The radius of a metal sphere is 3 cm. The sphere is melted and made into a long wire of uniform circular cross-section, whose length is 36 cm. To calculate the radius of wire, complete the following activity.
Radius of the sphere = `square`
Length of the wire = `square`
Let the radius of the wire by r cm.
Now, Volume of the wire = Volume of the `square`
`square` = `square`
r2 × `square` = `square` × `square`
r2 × `square` = `square`
r = `square`
Hence, the radius of the wire is `square` cm.
