Advertisements
Advertisements
Question
The dimensions of a metallic cuboid are 44 cm × 42 cm × 21 cm. it is molten and recast into a sphere. Find the surface area of the sphere.
Solution
The volume of cuboid = l × b × h
= (44 × 42 × 21) cm3
= 38808 cm3
Since, the metallic cuboid is molten and into a sphere,
volume of sphere = volume of cuboid
∴ volume of sphere = 38808 cm3
But, volume of sphere = `4/3 pir^3`
∴ `4/3 pir^3` = 38808
∴ `r^3 = 38808 xx 3/4 xx 7/22`
∴ r3 = 21 × 21 × 21
∴ r = 21 cm
∴ surface area of spher = 4πr2
= `4 xx 22/7 xx(21)^2`
= 5544 cm2
∴ the surface area of the sphere is 5544 cm2.
APPEARS IN
RELATED QUESTIONS
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
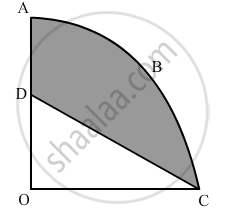
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
A tank of cylindrical shape has radius 2.8 m and its height 3.5 m. Complete the activity to find how many litres of water the tank will contain.
Capacity of water tank = Volume of cylindrical tank
= πr2h
Find the mass of a 3.5 m long lead pipe, if the external diameter of the pipe is 2.4 cm, thickness of the metal is 2 mm and the mass of 1 cm3 of lead is 11.4 grams.
The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its capacity in litres and the amount of sheet required to make this bucket.
The volume of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is
The diameters of two circular ends of the bucket are 44 cm and 24 cm . The height of the bucket is 35 cm . The capacity of the bucket is
A 5-m-wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of ₹25 per metre.
The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of diameter 2.8 cm. Find the length of the wire.
The volume of a cube is 729 cm3. Find its surface area.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total
surface area of the toy.
If each edge of a cube is increased by 50%, the percentage increase in the surface area is
πThe height of a cylinder is 14 cm and its curved surface area is 264 cm2. The volume of the cylinder is
The ratio of the total surface area to the lateral surface area of a cylinder with base radius 80 cm and height 20 cm is
The radius of the base and the height of a solid right circular cylinder are in the ratio 2 : 3 and its volume is 1617 cm3. Find the total surface area of the cylinder.
Find the surface area of a sphere of radius 3.5 cm.
Arrange the given objects according to their volume
The surface areas of two spheres are in the ratio 1 : 2. The ratio of their volume is ______.
A surahi is the combination of ______.
A cylindrical pencil sharpened at one edge is the combination of ______.
