Advertisements
Advertisements
प्रश्न
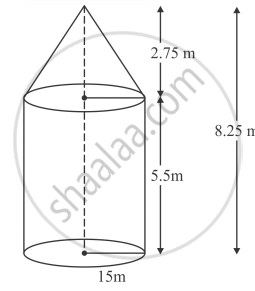
A tent of height 8.25 m is in the form of a right circular cylinder with diameter of base 30 m and height 5.5 m, surmounted by a right circular cone of the same base. Find the cost of the canvas of the tent at the rate of Rs 45 per m2.
उत्तर
`l = sqrt((2.75)^2) + (15)^2`
`l = sqrt(232.5625)`
`= 15 .25`
Total surface area of the tent
`=2 pirh + pirl`
`=pir(2h + l)`
`=22/7 xx 15[2 xx 5 -5 + 15.25]`
`= (330 xx 26.25)/7`
`=1237.5`
Therefore,
Cost of the canvas of the tent
`=1237.5 xx 45`
`= "Rs . 55687.50"`
APPEARS IN
संबंधित प्रश्न
The `3/4` th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each of the hemispherical ends is 7 cm, find the cost of polishing its surface at the rate of Rs 10 per dm2 .
Two spheres of same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere ?
A cubic cm of gold is drawn into a wire 0.1 mm in diameter, find the length of the wire.
The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108 m, find its diameter.
The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of diameter 2.8 cm. Find the length of the wire.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3 . the radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it.
A sphere and a cube have equal surface areas. The ratio of the volume of the sphere to that of cube is ______.
The surface areas of the six faces of a rectangular solid are 16, 16, 32, 32, 72 and 72 square centimetres. The volume of the solid, in cubic centimetres, is ______.
The radius of a metal sphere is 3 cm. The sphere is melted and made into a long wire of uniform circular cross-section, whose length is 36 cm. To calculate the radius of wire, complete the following activity.
Radius of the sphere = `square`
Length of the wire = `square`
Let the radius of the wire by r cm.
Now, Volume of the wire = Volume of the `square`
`square` = `square`
r2 × `square` = `square` × `square`
r2 × `square` = `square`
r = `square`
Hence, the radius of the wire is `square` cm.
