Advertisements
Advertisements
प्रश्न
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3 . the radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it.
उत्तर
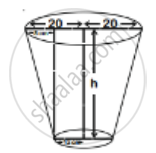
Let the height of the bucket ne h cm and Slant height be I cm.
Here,
r1 = 20 cm
r2 = 12 cm
And capacity of bucket = 12308.8 cm3
We know that capacity of bucket = `(pi"h")/3 (r_2^2 + r_2^2 + r_1r_2)`
`= 3.14 xx "h"/3 (400 + 144 + 240)`
`= 3.14xx"h"/3 xx 784`
So we have = `3.14xx"h"/3xx784` = 12308.8
`"h" = (12308.8xx3)/(3.14xx784)`
= 15 cm
Now, the slant height of the frustum,
l = `sqrt("h"^2 + ("r"_1 - "r"_2)^2`
`= sqrt(15^2 + 8^2)`
`=sqrt289`
= 17 cm
Area of metal sheet used in making it
`= pir_2^2 + pi(r_1 + r_2)^2`
`= 3.174 xx [144 + (20 + 12) xx 17]`
= 2160.32 cm2
APPEARS IN
संबंधित प्रश्न
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each of the hemispherical ends is 7 cm, find the cost of polishing its surface at the rate of Rs 10 per dm2 .
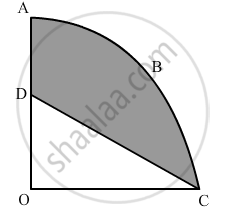
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
The diameter of a sphere is 6 cm. It is melted and drawn in to a wire of diameter 2 mm. The length of the wire is
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be \[\frac{1}{27}\] of the volume of the given cone, then the height above the base at which the section has been made, is
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
If three metallic spheres of radii 6 cm, 8 cm and 10 cm are melted to form a single sphere, the diameter of the sphere is
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
If the surface area of a sphere is 616 cm2, its diameter (in cm) is ______. (Taking π = `22/7`)
The total surface area of a cube is 864 cm2. Its volume is
The diameter of the base of a cylinder is 4 cm and its height is 14 cm. The volume of the cylinder is
