Advertisements
Advertisements
प्रश्न
Prove that in a right-angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
उत्तर
Given: A right triangle ABC in which ∠B = 90°
To Prove: (Hypotenuse)2 = (Base)2 + (perpendicular)2
i.e AC2 = AB2 + BC2
Construction: From B, Draw BD ⊥ AC
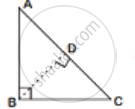
In ΔABC and ΔADB
∠BAC = ∠DAB [Common]
∠ABC = ∠ADB [each 90°]
∴ ΔABC ∼ ΔADB [By AA similarity]
`=> "AB"/"AC" = "AD"/"AB"`
`=> AB2 - AD x AC ...(i)
Similarity, ΔABC ∼ ΔBDC
`=> "BC"/"DC" = "AC"/"BC"`
`=> "BC"^2 - "AC" xx "DC"` ...(ii)
On adding (i) and (iii) we get
AB2 + BC2 = AD x AC + AC x DC
`=>` AB2 + BC2 = AC(AD + DC)
`=>` AB2 + BC2 = AC x AC
`=>` AC2 = AB2 + BC2
Notes
Δ
∠
APPEARS IN
संबंधित प्रश्न
The areas of two similar triangles ∆ABC and ∆PQR are 25 cm2 and 49 cm2 respectively. If QR = 9.8 cm, find BC
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
ABC is a triangle in which ∠A =90°, AN⊥ BC, BC = 12 cm and AC = 5cm. Find the ratio of the areas of ΔANC and ΔABC.
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
∆LMN ~ ∆PQR, 9 × A (∆PQR ) = 16 × A (∆LMN). If QR = 20 then Find MN.
In the given figure 1.66, seg PQ || seg DE, A(∆PQF) = 20 units, PF = 2 DP, then Find A(◻DPQE) by completing the following activity.

ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
In ΔLMN, ∠L = 50° and ∠N = 60°, If ΔLMN ~ ΔPQR, then find ∠Q.
