Advertisements
Advertisements
प्रश्न
Prove that in a right-angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
उत्तर
Given: A right triangle ABC in which ∠B = 90°
To Prove: (Hypotenuse)2 = (Base)2 + (perpendicular)2
i.e AC2 = AB2 + BC2
Construction: From B, Draw BD ⊥ AC
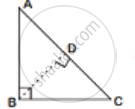
In ΔABC and ΔADB
∠BAC = ∠DAB [Common]
∠ABC = ∠ADB [each 90°]
∴ ΔABC ∼ ΔADB [By AA similarity]
`=> "AB"/"AC" = "AD"/"AB"`
`=> AB2 - AD x AC ...(i)
Similarity, ΔABC ∼ ΔBDC
`=> "BC"/"DC" = "AC"/"BC"`
`=> "BC"^2 - "AC" xx "DC"` ...(ii)
On adding (i) and (iii) we get
AB2 + BC2 = AD x AC + AC x DC
`=>` AB2 + BC2 = AC(AD + DC)
`=>` AB2 + BC2 = AC x AC
`=>` AC2 = AB2 + BC2
Notes
Δ
∠
APPEARS IN
संबंधित प्रश्न
Let Δ ABC ~ Δ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC
If the areas of two similar triangles are equal, prove that they are congruent.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
In figure below ΔACB ~ ΔAPQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm,
find CA and AQ. Also, find the area (ΔACB): area (ΔAPQ)

The areas of two similar triangles are 25 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 m, prove that area of ΔAPQ is one- sixteenth of the area of ABC.
If ΔABC and ΔBDE are equilateral triangles, where D is the mid-point of BC, find the ratio of areas of ΔABC and ΔBDE.
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area (ΔADE): Area (ΔABC) = 3: 4
If ∆ABC ~ ∆PQR, A (∆ABC) = 80, A (∆PQR) = 125, then fill in the blanks. \[\frac{A\left( ∆ ABC \right)}{A\left( ∆ . . . . \right)} = \frac{80}{125} \therefore \frac{AB}{PQ} = \frac{......}{......}\]
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
