Advertisements
Advertisements
प्रश्न
The areas of two similar triangles are 25 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other.
उत्तर
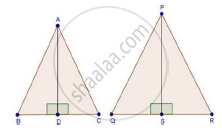
We have,
ΔABC ~ ΔPQR
Area (ΔABC) = 25 cm2
Area (ΔPQR) = 36 cm2
AD = 2.4 cm
And AD and PS are the altitudes
To find: PS
Proof: Since, ΔABC ~ ΔPQR
Then, by area of similar triangle theorem
`("Area"(triangleABC))/("Area"(trianglePQR))="AB"^2/"PQ"^2`
`rArr25/36="AB"^2/"PQ"^2`
`rArr5/6="AB"/"PQ"` .........(i)
In ΔABD and ΔPQS
∠B = ∠Q [Δ ABC ~ ΔPQR]
∠ADB ~ ∠PSQ [Each 90°]
Then, ΔABD ~ ΔPQS [By AA similarity]
`therefore"AB"/"PS"="AD"/"PS"` ......(ii) [Corresponding parts of similar Δ are proportional]
Compare (i) and (ii)
`"AD"/"PS"=5/6`
`rArr2.4/"PS"=5/6`
`"PS"=(2.4xx6)/5=2.88` cm
APPEARS IN
संबंधित प्रश्न
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
Let Δ ABC ~ Δ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC
In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(ar(ABC))/(ar(DBC)) = (AO)/(DO)`
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
In figure below ΔACB ~ ΔAPQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm,
find CA and AQ. Also, find the area (ΔACB): area (ΔAPQ)

The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find the length of QR.
∆LMN ~ ∆PQR, 9 × A (∆PQR ) = 16 × A (∆LMN). If QR = 20 then Find MN.
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
In ΔLMN, ∠L = 50° and ∠N = 60°, If ΔLMN ~ ΔPQR, then find ∠Q.
