Question

ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is

पर्याय

• 2 : 1

• 1 : 2

• 4 : 1

• 1 : 4

Answer 1

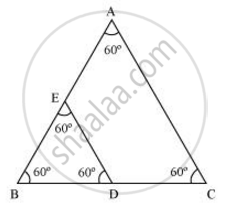
We know that equilateral triangles have all its angles as 60º and all its sides of the same length. Therefore, all equilateral triangles are similar to each other. Hence, the ratio between the areas of these triangles will be equal to the square of the ratio between the sides of these triangles.

Let side of ΔABC = x

Therefore, side of  ΔBDE = `x/2`

`∴ (area(ΔABC))/(area(ΔBDE)) = (x/(x/2))^2 =4/1`

Hence, the correct answer is (C).