Advertisements
Advertisements
प्रश्न
ABC is a triangle in which ∠A =90°, AN⊥ BC, BC = 12 cm and AC = 5cm. Find the ratio of the areas of ΔANC and ΔABC.
उत्तर
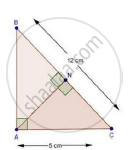
In ΔANC and ΔABC
∠C = ∠C [Common]
∠ANC = ∠BAC [Each 90°]
Then, ΔANC ~ ΔBAC [By AA similarity]
By area of similarity triangle theorem
`("Area"(triangleANC))/("Area"(triangleBAC))="AC"^2/"BC"^2`
`=5^2/12^2`
`=25/144`
APPEARS IN
संबंधित प्रश्न
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Triangles ABC and DEF are similar If AC = 19cm and DF = 8 cm, find the ratio of the area of two triangles.
The areas of two similar triangles are 81 cm2 and 49 cm2 respectively. Find the ratio of their corresponding heights. What is the ratio of their corresponding medians?
If ∆ABC ~ ∆PQR, A (∆ABC) = 80, A (∆PQR) = 125, then fill in the blanks. \[\frac{A\left( ∆ ABC \right)}{A\left( ∆ . . . . \right)} = \frac{80}{125} \therefore \frac{AB}{PQ} = \frac{......}{......}\]
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
If ∆XYZ ~ ∆PQR and A(∆XYZ) = 25 cm2, A(∆PQR) = 4 cm2 then XY : PQ = ?
In a rhombus if d1 = 16 cm, d2 = 12 cm, its area will be ______.
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
Find the length of ST, if ΔPQR ∼ ΔPST.

