Question

Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Answer 1

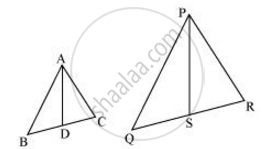
Let us assume two similar triangles as ΔABC ∼ ΔPQR. Let AD and PS be the medians of these triangles.

∵  ΔABC ∼ ΔPQR

:.(AB)/(PQ) = (BC)/(QR) = (AC)/(PR)...(1)

∠A = ∠P, ∠B = ∠Q, ∠C = ∠R … (2)

Since AD and PS are medians,

∴ BD = DC = `(BC)/2`

And, QS = SR = `(QR)/2`

Equation (1) becomes

(AB)/(PQ) = (BD)/(QS) = (AC)/(PR)  ....(3)

In ΔABD and ΔPQS,

∠B = ∠Q [Using equation (2)]

and (AB)/(PQ) = (BD)/(QS)    [Using equation (3)]

∴ ΔABD ∼ ΔPQS (SAS similarity criterion)

Therefore, it can be said that

`(AB)/(PQ) = (BD)/(QS) =(AD)/(PS) ....(4)`

`(ar(triangleABC))/(ar(trianglePQR)) = ((AB)/(PQ))^2 = ((BC)/(QR))^2 = ((AC)/(PR))^2`

From equations (1) and (4), we may find that

`(AB)/(PQ) = (BC)/(QR) = (AC)/(PR) = (AD)/(PS)`

And hence

`(ar(triangleABC))/(ar(trianglePQR)) = ((AD)/(PS))^2`