Advertisements
Advertisements
प्रश्न
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
उत्तर
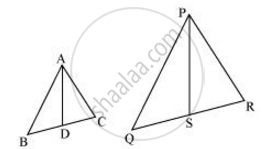
Let us assume two similar triangles as ΔABC ∼ ΔPQR. Let AD and PS be the medians of these triangles.
∵ ΔABC ∼ ΔPQR
:.(AB)/(PQ) = (BC)/(QR) = (AC)/(PR)...(1)
∠A = ∠P, ∠B = ∠Q, ∠C = ∠R … (2)
Since AD and PS are medians,
∴ BD = DC = `(BC)/2`
And, QS = SR = `(QR)/2`
Equation (1) becomes
(AB)/(PQ) = (BD)/(QS) = (AC)/(PR) ....(3)
In ΔABD and ΔPQS,
∠B = ∠Q [Using equation (2)]
and (AB)/(PQ) = (BD)/(QS) [Using equation (3)]
∴ ΔABD ∼ ΔPQS (SAS similarity criterion)
Therefore, it can be said that
`(AB)/(PQ) = (BD)/(QS) =(AD)/(PS) ....(4)`
`(ar(triangleABC))/(ar(trianglePQR)) = ((AB)/(PQ))^2 = ((BC)/(QR))^2 = ((AC)/(PR))^2`
From equations (1) and (4), we may find that
`(AB)/(PQ) = (BC)/(QR) = (AC)/(PR) = (AD)/(PS)`
And hence
`(ar(triangleABC))/(ar(trianglePQR)) = ((AD)/(PS))^2`
APPEARS IN
संबंधित प्रश्न
In two similar triangles ABC and PQR, if their corresponding altitudes AD and PS are in the ratio 4 : 9, find the ratio of the areas of ∆ABC and ∆PQR
In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(ar(ABC))/(ar(DBC)) = (AO)/(DO)`
If the areas of two similar triangles are equal, prove that they are congruent.
In ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.
Ratio of areas of two similar triangles is 9 : 25. _______ is the ratio of their corresponding sides.
O is a point on side PQ of a APQR such that PO = QO = RO, then ______.
ΔABC ~ ΔPQR. In ΔABC, AB = 5.4 cm, BC = 4.2 cm, AC = 6.0 cm, AB:PQ = 3:2, then construct ΔABC and ΔPQR.
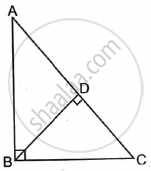
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
