Advertisements
Advertisements
प्रश्न
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals
उत्तर
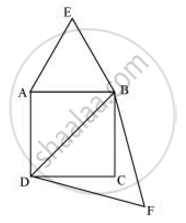
Let ABCD be a square of side a.
Therefore, its diagonal = `sqrt2a`
Two desired equilateral triangles are formed as ΔABE and ΔDBF.
Side of an equilateral triangle, ΔABE, described on one of its sides = a
Side of an equilateral triangle, ΔDBF, described on one of its diagonals = `sqrt2a`
We know that equilateral triangles have all its angles as 60º and all its sides of the same length. Therefore, all equilateral triangles are similar to each other. Hence, the ratio between the areas of these triangles will be equal to the square of the ratio between the sides of these triangles.
`"Area of Δ ABE"/"Area of ΔDBF"=(a/(sqrt2a))^2`
`"Area of Δ ABE"/"Area of ΔDBF"=(1/sqrt2)^2=1/2`
APPEARS IN
संबंधित प्रश्न
In a trapezium ABCD, O is the point of intersection of AC and BD, AB || CD and AB = 2 × CD. If the area of ∆AOB = 84 cm2 . Find the area of ∆COD
Let Δ ABC ~ Δ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
∆MNT ~ ∆QRS. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio `("A"(Δ"MNT"))/("A"(Δ"QRS"))`.
In the given figure DE || AC which of the following is true?
In ΔLMN, ∠L = 50° and ∠N = 60°, If ΔLMN ~ ΔPQR, then find ∠Q.
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
