Advertisements
Advertisements
प्रश्न
∆MNT ~ ∆QRS. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio `("A"(Δ"MNT"))/("A"(Δ"QRS"))`.
उत्तर

∆MNT ~ ∆QRS ...(Given)
∴ ∠M ≅ ∠Q ...(Corresponding angles of similar triangles)(i)
In ∆MLT and ∆QPS,
∠M ≅ ∠Q ...[From (i)]
∠MLT ≅ ∠QPS ...(Each angle is of measure 90°)
∴ ∆MLT ~ ∆QPS ...(AA test of similarity)
∴ `"MT"/"QS" = "TL"/"SP" ...("Corresponding sides of similar triangles")`
∴ `"MT"/"QS" = 5/9`
Now, ∆MNT ~ ∆QRS ...(ii) (Given)
By Theorem of areas of similar triangles,
∴ `("A"(∆"MNT"))/("A"(∆"QRS")) = "MT"^2/"QS"^2`
∴ `("A"(∆"MNT"))/("A"(∆"QRS")) = ("MT"/"QS")^2`
∴ `("A"(∆"MNT"))/("A"(∆"QRS")) = (5/9)^2` ...[From (ii)]
∴ `("A"(∆"MNT"))/("A"(∆"QRS")) = 25/81`
APPEARS IN
संबंधित प्रश्न
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the area of ΔDEF and ΔABC.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
The areas of two similar triangles are 81 cm2 and 49 cm2 respectively. Find the ratio of their corresponding heights. What is the ratio of their corresponding medians?
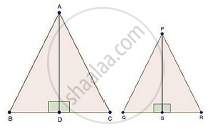
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
The areas of two similar triangles are 25 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find the length of QR.
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
Prove that in a right-angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In the given figure DE || AC which of the following is true?
In ΔLMN, ∠L = 50° and ∠N = 60°, If ΔLMN ~ ΔPQR, then find ∠Q.
In a rhombus if d1 = 16 cm, d2 = 12 cm, its area will be ______.
If the perimeter of two similar triangles is in the ratio 2 : 3, what is the ratio of their sides?
If ΔABC ∼ ΔPQR and `(A(ΔABC))/(A(ΔPQR)) = 16/25`, then find AB : PQ.
