Advertisements
Advertisements
प्रश्न
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
उत्तर
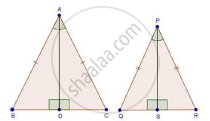
Given: AB = AC, PQ = PQ and ∠A = ∠P
And, AD and PS are altitudes
And, `("Area"(triangleABC))/("Area"(trianglePQR))=36/25` .........(i)
To find `"AD"/"PS"`
Proof: Since, AB = AC and PQ = PR
Then, `"AB"/"AC"=1` and `"PQ"/"PR"=1`
`therefore"AB"/"AC"="PQ"/"PR"`
`rArr"AB"/"PQ"="AC"/"PR"` ........(ii)
In ΔABC and ΔPQR
∠A = ∠P [Given]
`"AB"/"PQ"="AC"/"PR"` [From (2)]
Then, ΔABC ~ ΔPQR [By SAS similarity]
`therefore("Area"(triangleABC))/("Area"(trianglePQR))="AB"^2/"PQ"^2` .....(iii) [By area of similar triangle theorem]
Compare equation (i) and (iii)
`"AB"^2/"PQ"^2=36/25`
`"AB"/"PQ"=6/5` ..........(iv)
In ΔABD and ΔPQS
∠B = ∠Q [ΔABC ~ ΔPQR]
∠ADB = ∠PSQ [Each 90°]
Then, ΔABD ~ ΔPQS [By AA similarity]
`therefore"AB"/"PQ"="AD"/"PS"`
`rArr6/5="AD"/"PS"` [From (iv)]
APPEARS IN
संबंधित प्रश्न
In two similar triangles ABC and PQR, if their corresponding altitudes AD and PS are in the ratio 4 : 9, find the ratio of the areas of ∆ABC and ∆PQR
If ∆ABC ~ ∆DEF such that area of ∆ABC is 16cm2 and the area of ∆DEF is 25cm2 and BC = 2.3 cm. Find the length of EF.
Let Δ ABC ~ Δ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC
Triangles ABC and DEF are similar If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ΔABC and ΔDEF.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
In ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find the length of QR.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.
If ΔABC ∼ ΔPQR and `(A(ΔABC))/(A(ΔPQR)) = 16/25`, then find AB : PQ.
If ΔPQR ∼ ΔABC; PQ = 6 cm, AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is ______.
