Question

ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 m, prove that area of ΔAPQ is one- sixteenth of the area of ABC.

Answer 1

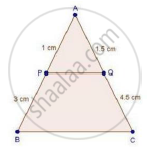
We have,

AP = 1 cm, PB = 3 cm, AQ = 1.5 cm and QC = 4.5 m

In ΔAPQ and ΔABC

∠A = ∠A                            [Common]

`"AP"/"AB"="AQ"/"AC"`           [Each equal to 1/4]

Then, ΔAPQ ~ ΔABC                  [By SAS similarity]

By area of similar triangle theorem

`("area"(triangleAPQ))/("area"(triangleABC))=1^2/4^2`

`rArr("area"(triangleAPQ))/("area"(triangleABC))=1^2/16xx"area"(triangleABC)`