Advertisements
Advertisements
प्रश्न
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 m, prove that area of ΔAPQ is one- sixteenth of the area of ABC.
उत्तर
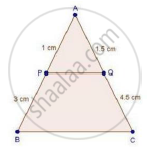
We have,
AP = 1 cm, PB = 3 cm, AQ = 1.5 cm and QC = 4.5 m
In ΔAPQ and ΔABC
∠A = ∠A [Common]
`"AP"/"AB"="AQ"/"AC"` [Each equal to 1/4]
Then, ΔAPQ ~ ΔABC [By SAS similarity]
By area of similar triangle theorem
`("area"(triangleAPQ))/("area"(triangleABC))=1^2/4^2`
`rArr("area"(triangleAPQ))/("area"(triangleABC))=1^2/16xx"area"(triangleABC)`
APPEARS IN
संबंधित प्रश्न
If the areas of two similar triangles are equal, prove that they are congruent.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, find the longest side of the smaller triangle.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
∆LMN ~ ∆PQR, 9 × A (∆PQR ) = 16 × A (∆LMN). If QR = 20 then Find MN.
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.
In the given figure, ΔACB ~ ΔAPQ. If AB = 6 cm, BC = 8 cm, and PQ = 4 cm then AQ is equal to ______.
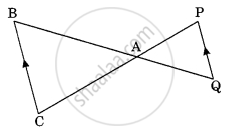
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.
In ΔABC, seg DE || side BC. If 2A(ΔADE) = A(⬜ DBCE), find AB : AD and show that BC = `sqrt(3)` DE.
If ΔABC ∼ ∆PQR and AB : PQ = 2 : 3, then find the value of `(A(triangleABC))/(A(trianglePQR))`.
