Advertisements
Advertisements
प्रश्न
∆LMN ~ ∆PQR, 9 × A (∆PQR ) = 16 × A (∆LMN). If QR = 20 then Find MN.
उत्तर
Given:
QR = 20
∆LMN ~ ∆PQR
9 × A (∆PQR ) = 16 × A (∆LMN)
Consider, 9 × A (∆PQR ) = 16 × A (∆LMN)
\[\frac{A\left( ∆ LMN \right)}{A\left( ∆ PQR \right)} = \frac{9}{16}\]
\[ \Rightarrow \frac{{MN}^2}{{QR}^2} = \frac{3^2}{4^2}\]
\[ \Rightarrow \frac{MN}{QR} = \frac{3}{4}\]
\[\Rightarrow MN = \frac{3}{4} \times QR\]
\[ \Rightarrow MN = \frac{3}{4} \times 20 \left[ \because QR = 20 \right]\]
\[ \Rightarrow MN = 15\]
APPEARS IN
संबंधित प्रश्न
If ∆ABC ~ ∆DEF such that area of ∆ABC is 16cm2 and the area of ∆DEF is 25cm2 and BC = 2.3 cm. Find the length of EF.
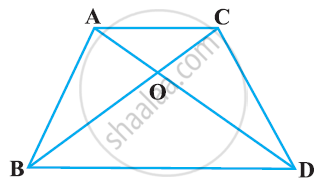
In a trapezium ABCD, O is the point of intersection of AC and BD, AB || CD and AB = 2 × CD. If the area of ∆AOB = 84 cm2 . Find the area of ∆COD
In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(ar(ABC))/(ar(DBC)) = (AO)/(DO)`
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
Triangles ABC and DEF are similar If AC = 19cm and DF = 8 cm, find the ratio of the area of two triangles.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, find the longest side of the smaller triangle.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
ABC is a triangle in which ∠A =90°, AN⊥ BC, BC = 12 cm and AC = 5cm. Find the ratio of the areas of ΔANC and ΔABC.
In Figure, DE || BC If DE = 4cm, BC = 8 cm and Area (ΔADE) = 25 cm2, find the area of ΔABC.
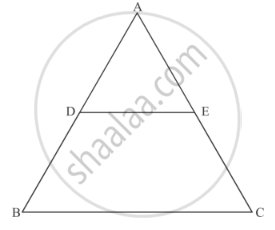
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
Prove that the points (2, −2), (−2, 1) and (5, 2) are the vertices of a right angled triangle. Also find the area of this triangleb ?
The ratio of corresponding sides of similar triangles is 3 : 5; then find the ratio of their areas.
∆MNT ~ ∆QRS. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio `("A"(Δ"MNT"))/("A"(Δ"QRS"))`.
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
Ratio of areas of two similar triangles is 9 : 25. _______ is the ratio of their corresponding sides.
In the given figure, ΔACB ~ ΔAPQ. If AB = 6 cm, BC = 8 cm, and PQ = 4 cm then AQ is equal to ______.
In a rhombus if d1 = 16 cm, d2 = 12 cm, its area will be ______.
Find the length of ST, if ΔPQR ∼ ΔPST.

In ΔABC, seg DE || side BC. If 2A(ΔADE) = A(⬜ DBCE), find AB : AD and show that BC = `sqrt(3)` DE.
