Advertisements
Advertisements
प्रश्न
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
उत्तर
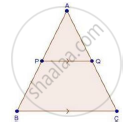
We have,
PQ || BC
And `"AP"/"PB"=1/2`
In ΔAPQ and ΔABC
∠A = ∠A [Common]
∠APQ = ∠B [Corresponding angles]
Then, ΔAPQ ~ΔABC [By AA similarity]
By area of similar triangle theorem
`("area"(triangleAPQ))/("area"(triangleABC))="AP"^2/"AB"^2`
`rArr("area"(triangleAPQ))/(("area"(triangleAPQ)+"area"("trap.BPQC")))=1^2/3^2` `["AP"/"PB"=1/2]`
⇒ 9ar (APQ) = ar(ΔAPQ) + ar(trap. BPQC)
⇒ 9ar (APQ) − ar(ΔAPQ) = ar(trap. BPQC)
⇒ 8ar(APQ) = ar(trap. BPQC)
`rArr("area"(triangleAPQ))/("area"("trap.BPQC"))=1/8`
APPEARS IN
संबंधित प्रश्न
In figure below ΔACB ~ ΔAPQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm,
find CA and AQ. Also, find the area (ΔACB): area (ΔAPQ)

ABC is a triangle in which ∠A =90°, AN⊥ BC, BC = 12 cm and AC = 5cm. Find the ratio of the areas of ΔANC and ΔABC.
If ΔABC ~ ΔDEF such that AB = 5 cm, area (ΔABC) = 20 cm2 and area (ΔDEF) = 45 cm2, determine DE.
The ratio of corresponding sides of similar triangles is 3 : 5; then find the ratio of their areas.
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
∆MNT ~ ∆QRS. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio `("A"(Δ"MNT"))/("A"(Δ"QRS"))`.
The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.
In ΔLMN, ∠L = 50° and ∠N = 60°, If ΔLMN ~ ΔPQR, then find ∠Q.
If ΔPQR ∼ ΔABC; PQ = 6 cm, AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is ______.
