Advertisements
Advertisements
प्रश्न
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
उत्तर
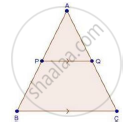
We have,
PQ || BC
And `"AP"/"PB"=1/2`
In ΔAPQ and ΔABC
∠A = ∠A [Common]
∠APQ = ∠B [Corresponding angles]
Then, ΔAPQ ~ΔABC [By AA similarity]
By area of similar triangle theorem
`("area"(triangleAPQ))/("area"(triangleABC))="AP"^2/"AB"^2`
`rArr("area"(triangleAPQ))/(("area"(triangleAPQ)+"area"("trap.BPQC")))=1^2/3^2` `["AP"/"PB"=1/2]`
⇒ 9ar (APQ) = ar(ΔAPQ) + ar(trap. BPQC)
⇒ 9ar (APQ) − ar(ΔAPQ) = ar(trap. BPQC)
⇒ 8ar(APQ) = ar(trap. BPQC)
`rArr("area"(triangleAPQ))/("area"("trap.BPQC"))=1/8`
APPEARS IN
संबंधित प्रश्न
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
In ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area (ΔADE): Area (ΔABC) = 3: 4
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
The ratio of corresponding sides of similar triangles is 3 : 5, then find the ratio of their areas.
If ΔABC is similar to ΔDEF such that 2 AB = DE and BC = 8 cm then EF is equal to ______.
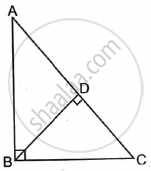
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.
In ΔABC, seg DE || side BC. If 2A(ΔADE) = A(⬜ DBCE), find AB : AD and show that BC = `sqrt(3)` DE.
If ΔABC ∼ ∆PQR and AB : PQ = 2 : 3, then find the value of `(A(triangleABC))/(A(trianglePQR))`.
