Advertisements
Advertisements
प्रश्न
If D is a point on the side AB of ΔABC such that AD : DB = 3.2 and E is a Point on BC such that DE || AC. Find the ratio of areas of ΔABC and ΔBDE.
उत्तर
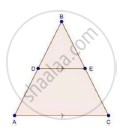
We have,
`"AD"/"DB"=3/2`
`rArr"DB"/"AD"2/3`
In ΔBDE and ΔBAC
∠B = ∠B [common]
∠ BDE = ∠A [corresponding angles]
Then, ΔBDE ~ ΔBAC [By AA similarity]
By area of similar triangle theorem
`("area"(triangleABC))/("area"(triangleBDE))="AB"^2/"BD"^2`
`=5^2/2^2` `["AD"/"DB"=3/2]`
`=25/4`
APPEARS IN
संबंधित प्रश्न
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
Let Δ ABC ~ Δ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC
Triangles ABC and DEF are similar If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
Triangles ABC and DEF are similar If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ΔABC and ΔDEF.
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other.
If ∆ABC ~ ∆PQR, A (∆ABC) = 80, A (∆PQR) = 125, then fill in the blanks. \[\frac{A\left( ∆ ABC \right)}{A\left( ∆ . . . . \right)} = \frac{80}{125} \therefore \frac{AB}{PQ} = \frac{......}{......}\]
In the given figure 1.66, seg PQ || seg DE, A(∆PQF) = 20 units, PF = 2 DP, then Find A(◻DPQE) by completing the following activity.

If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
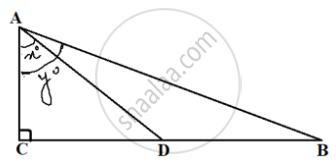
In the given figure, D is the mid-point of BC, then the value of `(coty^circ)/(cotx^circ)` is ______.
ΔABC ~ ΔPQR. In ΔABC, AB = 5.4 cm, BC = 4.2 cm, AC = 6.0 cm, AB:PQ = 3:2, then construct ΔABC and ΔPQR.
